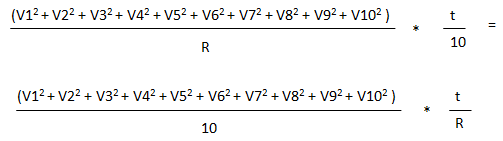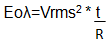Τι είναι η τάση rms και πως υπολογίστηκε

H εναλλασσόμενη τάση όπως είναι γνωστό δεν έχει σταθερή τιμή αλλά μεταβάλλεται με το χρόνο. Πως λοιπόν τα πολύμετρα μας δείχνουν μια συγκεκριμένη τιμή;

Σε αυτό το άρθρο θα δούμε ποια είναι η τάση rms (ενεργός τιμή) στο εναλλασσόμενο ρεύμα και γιατί είναι αυτή που μετράνε τα πολύμετρα.

Το ακρωνύμιο RMS σημαίνει Root Means Square (τετραγωνική ρίζα του μέσου όρου τετραγώνων) και όταν μιλάμε για εναλλασσόμενη τάση είναι η ισοδύναμη συνεχής τάση που δίνει τα ίδια θερμικά αποτελέσματα. Δηλαδή αν σε μια αντίσταση εφαρμόσουμε τάση 230VAC RMS θα τη ζεστάνει το ίδιο με μιά συνεχή τάση 230VDC.

Στο παρακάτω σχήμα έχουμε μια μπαταρία 20V συνδεδεμένη με μια λάμπα 10Ωμ.
Η ενέργεια που καταναλώνεται από την λάμπα για κάποιο χρόνο t θα είναι:  Ε=P*T=(V2/R)*t= (202/10)*t=40*t  και αν θεωρήσουμε ότι το t=1 ώρα, τότε Ε=40Wh (βατώρες)

Ταυτόχρονα έχουμε έναν εναλλακτήρα που παράγει εναλλασσόμενη τάση κορυφής (μέγιστη) 20V, συνδεδεμένο σε μια ίδια λάμπα 10Ωμ.
Θα δείξουμε ότι η ενέργεια που καταναλώνεται από την λάμπα για τον ίδιο χρόνο t δεν θα είναι  η ίδια με την προηγούμενη περίπτωση.

Ο λόγος που συμβαίνει αυτό είναι ότι η παραγόμενη τάση από μια πηγή συνεχούς ρεύματος (μπαταρία) έχει συνεχώς σταθερή τιμή 20V, ενώ στην ημιτονοειδή κυματομορφή της γεννήτριας αρχίζει από το μηδέν, αυξάνει μέχρι τη μέγιστη τιμή 20V και κατόπιν μηδενίζεται στο ίδιο χρονικό διάστημα.

Αφού η ημιτονοειδής κυματομορφή παίρνει την τιμή 20V για μικρό χρονικό διάστημα, ενώ το μεγαλύτερο διάστημα διατηρείται σε χαμηλότερα επίπεδα, δεν μπορεί να αναπτύξει την ίδια ισχύ με τα σταθερά 20V DC.

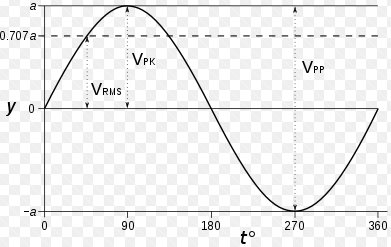
Χωρίζω την ημιτονοειδή τάση σε πάρα πολλά ίσα τμήματα (εδώ τα χωρίζω σε 10). To κάνω για τη θετική ημιπερίοδο της τάσης, το ίδιο θα ήταν για την αρνητική.

Αν μπορούσαμε να μετρήσουμε σε κάθε τμήμα την τάση που θα έχω θα βρίσκαμε:

V1=6,2V
V2=11,8V
V3=16,2V
V4=19V
V5=20V
V6=19V
V7=16,2V
V8=11,8V
V9=6,2V
V10=0V

Η ενέργεια που καταναλώνεται στην λάμπα αντίστασης R κάθε χρονική στιγμή t/10 από τις 10 που χώρισα το χρόνο t, θα είναι: Aπό τον τύπο Ε=P*t=(V2/R)*t , όπου
Ρ: ισχύς
V: τάση

Ε1=(V12/R)*(t/10)
Ε2=(V22/R)*(t/10)
Ε3=(V32/R)*(t/10)
Ε4=(V42/R)*(t/10)
Ε5=(V52/R)*(t/10)
Ε6=(V62/R)*(t/10)
Ε7=(V72/R)*(t/10)
Ε8=(V82/R)*(t/10)
Ε9=(V92/R)*(t/10)
Ε10=(V102/R)*(t/10)

Η ολική ενέργεια που καταναλώνεται στην αντίσταση R για όλο το χρονικό διάστημα t θα είναι:
Εολ=Ε1+Ε2+Ε3+Ε4+Ε5+Ε6+Ε7+Ε8+Ε9+Ε10 =

Eπίσης η ολική ενέργεια που καταναλώνεται στην αντίσταση R για όλο το χρονικό διάστημα t και που είναι αποτέλεσμα μιας ολικής τάσης που θα την ονομάσουμε rms θα είναι:
 Εολ=(Vrms2/R)*t  ή 

Από τις δύο παραπάνω εξισώσεις για την Εολ θα έχω:

H εναλλασσόμενη τάση λοιπόν Vrms που είναι υπεύθυνη για την κατανάλωση της ίδιας ενέργειας στην αντίσταση R με αυτή της συνεχούς τάσης Vdc θα είναι Vrms = 0,7071*Vmax=0,7071*20V=14,14V

Άρα η ενέργεια που καταναλώνεται, στην περίπτωση εναλλασσόμενης τάσης, από την λάμπα για κάποιο χρόνο t θα είναι  Ε=(Vrms2/R)*t= (14,142/10)*t=19,99*t  και αν θεωρήσουμε ότι το t=1 ώρα, τότε Ε=19,99Wh (βατώρες)

Τα απλά πολύμετρα λοιπόν μετράνε την μέγιστη τιμή της τάσης και παραβλέποντας την παραπάνω μαθηματική ανάλυση πολλαπλασιάζουν την τιμή αυτή με το 0,7071.

Ο τρόπος όμως αυτός ισχύει σε καθαρά ημιτονική τάση. Σε περίπτωση όμως που υπάρχει παραμόρφωση, μετατόπιση (συνεχής συνιστώσα) ή άλλη μορφή κυματομορφής χρειάζεται μέτρηση μέσω μετατροπέα πραγματικού RMS (true rms converter) που χρησιμοποιούν τα πολύμετρα τιμής (True-RMS).