Έλεγχος PLC logo 8 από Η/Υ

Στην ερώτηση αν μπορώ από τον Υπολογιστή μου, να ελέγξω τις εξόδους ενός PLC, επομένως να χειριστώ φορτία απομακρυσμένα η απάντηση είναι ΝΑΙ μάλιστα χωρίς κανένα επιπλέον κόστος απλά με ένα LOGO!8 και έναν υπολογιστή που τον μετατρέπω σε οθόνη HMI-SCADA,

H δημιουργία της οθόνης στον υπολογιστή ως HMI έγινε με το πρόγραμμα EasyBuilder Pro της εταιρείας Weintek το οποίο είναι εντελώς δωρεάν και μπορείτε να το κατεβάσετε από την σελίδα τους και συνδέεται με όλα τα PLC της αγοράς.

Δείτε το βίντεο παρακάτω:

πηγή:dimathanasopoulos.com

ΑΥΤΟΜΑΤΙΣΜΟΙ ΚΙΝΗΤΗΡΩΝ ΜΕ PLC

1o κύκλωμα

Εκκίνηση και αλλαγή φοράς περιστροφής τριφασικού κινητήρα υπό πλήρη τάση

2o κύκλωμα

Εκκίνηση και αλλαγή φοράς περιστροφής τριφασικού κινητήρα με αυτοματισμό αστέρα-τριγώνου

3o κύκλωμα

Εκκίνηση και αλλαγή φοράς περιστροφής τριφασικού κινητήρα υπό πλήρη τάση . Σταμάτημα του κινητήρα με 2 τρόπους, ελεύθερα με διακοπή της τάσης και με φρενάρισμα του άξονα

4o κύκλωμα

Εκκίνηση τριφασικού κινητήρα και αυτόματη αλλαγή φοράς περιστροφής χωρίς σταμάτημα

Τα παραπάνω για να πραγματοποιηθούν με κλασσικό αυτοματισμό χρειάζονται 10 ρελέ ισχύος, 2 χρονικά, πολλές βοηθητικές επαφές και περίπλοκες συνδεσμολογίες.

Με τη βοήθεια του PLC γίνεται  μόνο με 6 ρελέ ισχύος και με απλή συνδεσμολογία.

Δείτε στο video πως γίνεται

ΠΡΟΣΤΑΣΙΑ ΗΛΕΚΤΡΙΚΟΥ ΚΙΝΗΤΗΡΑ ΑΠΟ ΜΠΛΟΚΑΡΙΣΜΑ ΑΞΟΝΑ ΜΕ PLC

Ένα θερμικό προστατεύει τον ηλεκτρικό κινητήρα εναλλασσομένου ρεύματος από υπερφόρτιση. Ένα όμως κοινό θερμικό ίσως να μην προλάβει να αντιδράσει έγκαιρα σε περίπτωση που μπλοκάρει ο άξονας του κινητήρα. Σε αυτή την περίπτωση μια φθηνή και αξιόπιστη λύση είναι να χρησιμοποιήσουμε ένα φθηνό φωτοκύτταρο ή μαγνητικό διακόπτη που να ανιχνεύει την περιστροφή του άξονα του κινητήρα. Το παρακάτω κύκλωμα γίνεται με κλασσικό αυτοματισμό ή με τη βοήθεια ενός PLC, όπως στο παρακάτω video.

ΚΥΚΛΩΜΑΤΑ ΦΩΤΙΣΜΟΥ ΟΙΚΙΑΣ ΜΕ PLC

Κυκλώματα διακοπτών φωτισμού-αυτόματου κλιμακοστασίου-ηλεκτρικής κλειδαριάς με κωδικό. Όλα αυτά προγραμματιζόμενα με PLC σε γλώσσα FBD

ΟΙ λειτουργίες που πραγματοποιήθηκαν είναι οι παρακάτω:

Κύκλωμα  κλιμακοστασίου:

Πατώντας οποιοδήποτε μπουτόν ορόφου ανάβουν οι λάμπες του κλιμακοστασίου για 20 sec. Όταν ο χρόνος φτάσει στα 15 sec έχουμε στιγμιαίο αναβόσβημα των λαμπών για να μας προειδοποιήσει ότι υπολείπονται ακόμα 5 sec για να σβήσουν οι λάμπες. Αν ξαναπατήσω οποιοδήποτε μπουτόν ο χρόνος ανανεώνεται.

Επίσης αν πατήσω παρατεταμένα οποιοδήποτε από τα μπουτόν, οι λάμπες παραμένουν μόνιμα αναμμένες. Αν ξαναπατήσω παρατεταμένα τότε οι λάμπες μένουν αναμμένες για όσο χρόνο έχουμε ρυθμίσει τον αυτόματο και σβήνουν.

Κύκλωμα διπλού αλερετούρ με δύο μπουτόν που ελέγχει ένα τρίφωτο:

Με ένα πάτημα οποιουδήποτε μπουτόν ελέγχουμε τη μια λάμπα του τρίφωτου.

Με δύο συνεχόμενα πατήματα οποιουδήποτε μπουτόν ελέγχουμε τις άλλες δύο λάμπες του τρίφωτου.

Κύκλωμα κομμιτατέρ με ένα μπουτόν που ελέγχει ένα τρίφωτο:

Με ένα πάτημα του μπουτόν ελέγχουμε τη μια λάμπα του τρίφωτου.

Με παρατεταμένο πάτημα του μπουτόν ελέγχουμε τις άλλες δύο λάμπες του τρίφωτου.

Κύκλωμα αλερετούρ με τρία μπουτόν που ελέγχουν ένα απλό φωτιστικό

Με ένα πάτημα οποιουδήποτε από τα μπουτόν ελέγχουμε το απλό φωτιστικό

Κύκλωμα WC

Με ένα πάτημα του μπουτόν ανάβει ή σβήνει μόνο το φωτιστικό.

Με παρατεταμένο πάτημα του μπουτόν ανάβει το φωτιστικό και ο εξαεριστήρας.

Ξαναπατώντας παρατεταμένα σβήνει  το φωτιστικό και ο εξαεριστήρας εξακολουθεί να δουλεύει για 20 sec.

Κύκλωμα μπουτόν πανικού

Με πάτημα του μπουτόν αναβοσβήνουν όλα τα φώτα και χτυπάει διακεκομμένα μια σειρήνα.

Κύκλωμα close all με ένα μπουτόν

Με ένα πάτημα του μπουτόν σβήνουν όλα τα φωτιστικά που τυχόν είναι αναμμένα.

Κύκλωμα ηλεκτρικής κλειδαριάς με κωδικό αποτελούμενο από 7 απλά μπουτόν (αριθμημένα από το 1 έως το 6 και ένα μπουτόν reset).

Βάζοντας το σωστό κωδικό μέσα σε 2 sec, με τη βοήθεια των μπουτόν,  ανοίγει η ηλεκτρική κλειδαριά για 3 sec.

 Αν βάλω λάθος κωδικό τότε χτυπάει μια σειρήνα για 4 sec.

Δείτε το σχετικό video

Κανόνες μετατροπής σχεδίων κλασσικών κυκλωμάτων αυτοματισμού σε γλώσσα FBD μέσα από παραδείγματα

Τι είναι το PLC (Programmable Logic Controller)
 
Η προγραμματιζόμενη μονάδα λογικού ελέγχου ή προγραμματιζόμενος λογικός ελεγκτής (PLC), είναι ένας ψηφιακός υπολογιστής που χρησιμοποιείται για την αυτοματοποίηση των ηλεκτρομηχανολογικών διαδικασιών. Η μεγαλύτερη ίσως διαφοροποίησή τους είναι ότι στα PLC τα κυκλώματα αυτοματισμού δεν υλοποιούνται με την γνωστή (συρματωμένη τεχνική) αλλά με πρόγραμμα φορτωμένο στη μνήμη του (προγραμματιζόμενη τεχνική). Τα PLC δηλαδή είναι μικρουπολογιστικά συστήματα, που με το κατάλληλο προγραμματισμό λογικών εξισώσεων, επιλύουν προβλήματα αυτοματοποίησης. Με άλλα λόγια είναι μια κατηγορία συσκευών που η λειτουργία του βασίζεται στην χρήση μικροεπεξεργαστών ανάλογων με αυτούς που χρησιμοποιούνται στους ηλεκτρονικούς υπολογιστές. Τα PLC βρίσκουν εφαρμογή στην υλοποίηση και τον έλεγχο σύνθετων αλλά και απλούστερων κυκλωμάτων αυτοματισμού.

Γλώσσες Προγραμματισμού

Όταν αναφερόμαστε σε ένα PLC, ο προγραμματισμός είναι μια από τις βασικές έννοιες που μας έρχονται στο μυαλό. Τι είναι όμως ουσιαστικά ο προγραμματισμός και πως υλοποιείται από την εκάστοτε γλώσσα προγραμματισμού;
Προγραμματισμός είναι το σύνολο των διαδικασιών σύνταξης ενός υπολογιστικού προγράμματος για την πραγματοποίηση εργασιών ή για την επίλυση ενός δεδομένου προβλήματος. Ο προγραμματισμός περιλαμβάνει επίσης τον έλεγχο του προγράμματος για την επαλήθευση της ακρίβειάς του, και την προπαρασκευή των οδηγιών με τις οποίες ένας υπολογιστής θα εκτελέσει τις εργασίες που καθορίζονται στις προδιαγραφές του προγράμματος. Θεμελιώδη ρόλο στον υπολογιστικό προγραμματισμό διαδραματίζουν οι χιλιάδες γλώσσες προγραμματισμού, δηλαδή οι κώδικες επικοινωνίας οι οποίοι είναι απαραίτητοι για την δημιουργία ενός προγράμματος.
Με πιο απλά λόγια, προγραμματισμός ενός PLC σημαίνει να δημιουργήσουμε μια σειρά από εντολές οι οποίες λύνουν έναν συγκεκριμένο αλγόριθμο που αντιστοιχεί σε μια λειτουργία ενός συστήματος αυτοματισμού. Η διαδικασία που ακολουθείται για να γράψουμε αυτές τις εντολές αποτελεί το πρόγραμμα.

Κάθε PLC ακολουθεί συγκεκριμένες γλώσσες προγραμματισμού σύμφωνα με την αρχιτεκτονική του hardware. Θεωρητικά θα μπορούσαμε να προγραμματίσουμε ένα PLC γράφοντας εντολές σε μια γλώσσα μηχανής, κάτι που θα καθιστούσε όμως το PLC δύσκολο στον προγραμματισμό του και μόνο από ανθρώπους με βαθιά γνώση στην δομή και την λειτουργία των διαφόρων επεξεργαστών. Ως εκ τούτου λοιπόν, οι κατασκευαστές του, πρότειναν γλώσσες προγραμματισμού οι οποίες μπορούν να χρησιμοποιηθούν από ανθρώπους που σχετίζονται με τον έλεγχο συστημάτων.

Οι γλώσσες προγραμματισμού διακρίνονται σε γραφικές και μη γραφικές, ανάλογα με το είδος των στοιχείων που χρησιμοποιούν οι οποίες υπακούουν στα διεθνή πρότυπα IEC 1131-3..
Οι γραφικές χρησιμοποιούν γραφικά στοιχεία που μοιάζουν αρκετά με τα σύμβολα που χρησιμοποιούνται στον κλασικό αυτοματισμό και με τα σύμβολα λογικών πυλών (AND, NOT, OR, XOR, κλπ). Οι μη γραφικές χρησιμοποιούν εντολές που η κάθε μία αντιστοιχεί σε μια εντολή της γλώσσας μηχανής. Οι γραφικές είναι πιο προσιτές σε ανθρώπους που έχουν εμπειρία στον κλασικό αυτοματισμό.
Συνεπώς η επιλογή της κατάλληλης γλώσσας εξαρτάται από την γνώση και την εμπειρία του εκάστοτε χρήστη στην αντίστοιχη γλώσσα ή σε γλώσσα με παρόμοια λογική. Παράλληλα ο χρήστης οφείλει να είναι γνώστης ψηφιακών ηλεκτρονικών, συστημάτων αυτοματισμού και ηλεκτρονικών υπολογιστών.

Οι βασικές γλώσσες προγραμματισμού ενός PLC είναι οι παρακάτω:

• LAD: Ladder Diagram ή διάγραμμα Επαφών
• STL: Statement List ή Λίστα Εντολών
• FBD: Function Block Diagram ή Γλώσσα Λογικών Γραφικών
 
Ladder: Η γλώσσα Ladder είναι η πρώτη γλώσσα που αναπτύχθηκε και επιτρέπει την μεταφορά του ηλεκτρολογικού σχεδίου μέσω του H/Y στο PLC. Χρησιμοποιεί τα αμερικάνικα σύμβολα των επαφών και ανήκει στην κατηγορία των γραφικών γλωσσών μηχανής.

STL: Ανήκοντας στις μη γραφικές γλώσσες, η STL είναι μια γλώσσα προγραμματισμού σε μορφή κειμένου. Έχει την ικανότητα βέλτιστης χρήσης της μνήμης και εκτέλεσης του προγράμματος. Δημιουργεί μια λίστα προγράμματος με εντολές οι οποίες αντιστοιχούν στις λογικές πύλες (AND, OR, NOT κλπ) τοποθετημένες σε γραμμές η μία κάτω από την άλλη οι οποίες καταχωρούνται με συντομογραφικό τρόπο. Σε κάθε γραμμή περιέχονται δύο στοιχεία, η εντολή και η μεταβλητή. Η εντολή, αναγράφεται με λατινικούς χαρακτήρες και μπορεί να είναι είτε εντολή φόρτωσης (Load, LD), είτε εντολή από τις εκφράσεις της άλγεβρας Boole, είτε έτοιμη ρουτίνα του ελεγκτή (πχ, χρονιστής). Η μεταβλητή συνήθως περιέχει την διεύθυνση κάποιας εισόδου ή εξόδου. Παρόλο που στην αρχή η λίστα εντολών ήταν αρκετά φτωχή και περιοριζόταν μόνο στις βασικές λογικές εντολές , σήμερα έχει εξελιχθεί πάρα πολύ και συναντά κανείς σε αυτές στοιχεία από τις γλώσσες των υπολογιστών και κυρίως των γλωσσών Assembly.

FBD: Και αυτή η γλώσσα είναι γραφική, αλλά αντί του ηλεκτρολογικού σχεδίου του αυτοματισμού, χρησιμοποιεί το αντίστοιχο λογικό κύκλωμα. Ο τρόπος αυτός χρησιμοποιεί τα λογικά σύμβολα των λογικών πυλών της άλγεβρας Βοοle με τα οποία σχεδιάζουμε λογικά κυκλώματα, CSF. SFC: είναι μια γραφική γλώσσα προγραμματισμού. Είναι μια παράλληλη γλώσσα στην οποία πολλαπλές ροές ελέγχου μπορούν να είναι ενεργές ταυτόχρονα.

Στα περισσότερα PLC  δίνεται η δυνατότητα να προγραμματίζονται και με τις τρεις τεχνικές (γλώσσες). Η επιλογή της τεχνικής δηλαδή είναι θέμα μόνο του εκάστοτε προγραμματιστή. Επίσης σημαντικό γεγονός είναι και η συμβατότητα των τριών τεχνικών. Δηλαδή το πρόγραμμα της μιας τεχνικής  μετατρέπεται αμέσως σε πρόγραμμα της άλλης τεχνικής.

Εμείς στο άρθρο αυτό θα ασχοληθούμε μέσα από παραδείγματα με τη γλώσσα λογικών γραφικών FBD και τη χρησιμοποίησή της για τη μετατροπή ηλεκτρολογικών σχεδίων αυτοματισμού σε σχέδια με λογικές πύλες. Βέβαια εδώ να πούμε ότι το ηλεκτρολογικό σχέδιο ενός αυτοματισμού δεν είναι απαραίτητο ώστε να αναπτυχθεί ένα πρόγραμμα σε FBD. Μπορούμε να δημιουργήσουμε ένα κύκλωμα αυτοματισμού σε γλώσσα λογικών γραφικών με τη βοήθεια της άλγεβρας Boole και με αρκετή εμπειρία πολύ πιο εύκολα από το να μετατρέψουμε ένα έτοιμο ηλεκτρολογικό σχέδιο στη γλώσσα αυτή. Αυτό όμως είναι ένα άλλο κομμάτι που δεν θα ασχοληθούμε εδώ. Δεν θα ασχοληθούμε δηλαδή με τη δημιουργία αλλά με τη μετατροπή.

Οι εταιρείες κατασκευής PLC στην αρχή απέφευγαν να υιοθετήσουν αυτή τη γλώσσα γιατί το τεχνικό κατεστημένο της βιομηχανίας δεν είχε γνώσεις πάνω στα λογικά κυκλώματα. Σήμερα βέβαια αυτό έχει αλλάξει και οι τεχνικοί είναι γνώστες των λογικών διαγραμμάτων με αποτέλεσμα όλες οι εταιρείες πλέον να έχουν υιοθετήσει και αυτή τη γλώσσα στον προγραμματισμό των PLC που κατασκευάζουν.

Αυτό που χρειαζόμαστε να ξέρουμε για τη μετατροπή ενός κυκλώματος αυτοματισμού σε γλώσσα FBD είναι η κατανόηση και η λειτουργία των παρακάτω τριών λογικών πυλών.
Μία λογική πύλη είναι ηλεκτρονικό κύκλωμα το οποίο πραγματοποιεί μία λογική πράξη στις εισόδους της και παράγει μία έξοδο. Οι λογικές πύλες έχουν δημιουργηθεί για να δουλεύουν στο δυαδικό σύστημα.
Οι λογικές είναι ηλεκτρονικά κυκλώματα που σήμερα κυκλοφορούν σε ολοκληρωμένη μορφή (ολοκληρωμένα κυκλώματα)

Σε κάθε πύλη μπορούμε να δούμε:
Τους ακροδέκτες τροφοδοσίας του ολοκληρωμένου κυκλώματος. Τους ακροδέκτες εισόδων και τον ακροδέκτη της εξόδου

Στις εισόδους εφαρμόζεται ηλεκτρική τάση που μπορεί να πάρει δύο τιμές:
‘’Λογικό 1’’ όταν εφαρμόζεται τάση π.χ 5V DC ανάλογα με το είδος των ολοκληρωμένων κυκλωμάτων.
‘’Λογικό 0’’ όταν εφαρμόζεται τάση 0V
Στην πράξη το λογικό ‘’1’’ αντιστοιχεί σε τάσεις 3.5V - 5V, ενώ το λογικό ‘’0’’ σε τάσεις 0V – 1.5V.
Οι είσοδοι μετατρέπουν το ηλεκτρικό σήμα σε μια λογική ψηφιακή κατάσταση “0” ή “1” και οι έξοδοι μετατρέπουν μια λογική ψηφιακή κατάσταση σε ηλεκτρικό σήμα

Οι βασικές πύλες που αντιστοιχούν στις τρεις θεμελιώδεις λογικές πράξεις και τις οποίες χρειαζόμαστε είναι:

ΠΥΛΗ AND (ΚΑΙ)

 Οι λογικές μεταβλητές που συνδέονται με την λογική πράξη AND, δίνουν αποτέλεσμα αληθή, τότε και μόνον τότε όταν όλες οι λογικές μεταβλητές είναι αληθείς. Δηλαδή η πύλη AND θα βγάλει έξοδο ‘’1’’ μόνον όταν όλες οι είσοδοι δώσουν σήμα ‘’1’’.

ΠΥΛΗ OR (ή)

Η έξοδος της πύλης OR έχει λογική κατάσταση ‘’1’’ όταν τουλάχιστον μία από τις εισόδους της έχει λογική κατάσταση ‘’1’’. Ή διαφορετικά η έξοδος της πύλης OR έχει λογική κατάσταση ‘’0’’ όταν όλες οι είσοδοι της πύλης έχουν λογική κατάσταση ‘’0’’.

 ΠΥΛΗ ΝΟΤ (άρνηση)

 Η λογική πράξη NOT, εφαρμόζεται σε μια μόνο μεταβλητή και δίνει αποτέλεσμα αληθή, μόνο όταν η ίδια είναι ψευδής. Δηλαδή όταν η είσοδος της ΝΟΤ έχει τιμή ‘’1’’ η έξοδος έχει τιμή ‘’0’’ και αντίστροφα.

Ας ξεκινήσουμε λοιπόν με το τι  είναι οι είσοδοι και οι έξοδοι σε ένα PLC
 
Ο σκοπός των ψηφιακών εισόδων είναι να ενημερώνουν συνεχώς τη CPU (κεντρική μονάδα επεξεργασίας) του PLC για την κατάσταση του συστήματος. Αν δηλαδή έχει ενεργοποιηθεί κάποια διεργασία ή αν ο χειριστής ενεργοποίησε κάποιο διακόπτη. Αυτά τα δεδομένα μεταφέρονται μέσω ηλεκτρικού σήματος σε κλέμμες της συστοιχίας εισόδων, επεξεργάζονται και αποθηκεύονται στη μνήμη αναπαράστασης εισόδων.

Ο σκοπός των ψηφιακών εξόδων είναι να λαμβάνουν τις αποφάσεις της CPU και να τις μετατρέπουν σε εντολές προς το σύστημα. Αυτές οι αποφάσεις βρίσκονται αποθηκευμένες στη μνήμη αναπαράστασης των εξόδων της CPU και κατόπιν μορφοποιούνται σε ηλεκτρικά σήματα από τις μονάδες εξόδων. Οι μονάδες εξόδων δουλεύουν σαν διακόπτες παίρνοντας ή όχι τάση από την υλοποίηση του προγράμματος που εκτελεί η CPU. Όταν κλείσει ο διακόπτης το σήμα περνά προς το υπόλοιπο σύστημα.

Οι αναλογικές είσοδοι υλοποιούν παρόμοια λειτουργία με τις μονάδες ψηφιακών εισόδων. Βέβαια σε αυτή τη περίπτωση μπορούν να διαβαστούν συνεχείς τιμές τάσης. Αυτό σημαίνει ότι μια μονάδα αναλογικών εισόδων αντιλαμβάνεται τις τιμές ενός αναλογικού σήματος π.χ. εύρους 0-10V και τις αντιστοιχεί με ένα ακέραιο αριθμό από 0-255. Βέβαια πριν τις αναλογικές εισόδους θα πρέπει να παρεμβάλλεται ένας μετατροπέας σήματος, ώστε το σήμα να παίρνει αποδεκτές τιμές τάσης ή έντασης οι οποίες θα είναι κατανοητές από τη μονάδα εισόδων.

Οι αναλογικές έξοδοι λειτουργούν κατά αντιστοιχία με τις μονάδες ψηφιακών εξόδων. Ο ρόλος τους είναι να μετατρέψουν το δυαδικό αριθμητικό μέγεθος από τη CPU του λογικού ελεγκτή σε σήμα αντίστοιχης τάσης ή έντασης ρεύματος, με σκοπό την απευθείας ενεργοποίηση συνδεδεμένων μηχανών. Τα χαρακτηριστικά των αναλογικών εξόδων βρίσκονται σε πλήρη αρμονία με αυτά των αναλογικών εισόδων μιας και εκτελούν την αντίστροφη λειτουργία. Πάντα σε συνεργασία με το πρόγραμμα αυτοματισμού.

Ποια εξαρτήματα ενός αυτοματισμού θεωρούμε σαν εισόδους και ποια σαν εξόδους και πως τα χαρακτηρίζουμε κατά τη μετατροπή ενός κυκλώματος κλασσικού αυτοματισμού σε γλώσσα FBD;
 
ΕΙΣΟΔΟΙ: Είναι όλα τα εξαρτήματα ενός αυτοματισμού που δίνουν εντολή. Τέτοια είναι τα μπουτόν, οι διακόπτες, τερματικά και όλα τα αισθητήρια (οι βοηθητικές επαφές τους) όπως θερμικά, φωτοκύτταρα, ανιχνευτές κίνησης κλπ.
Τις εισόδους τις χαρακτηρίζουμε με το γράμμα Ι και με ένα αύξοντα αριθμό ανάλογα σε ποια είσοδο του PLC θα το βάλουμε, δηλαδή Ι1, Ι2, Ι3…κοκ.

ΕΞΟΔΟΙ: Είναι όλοι οι καταναλωτές. Τέτοιοι είναι τα ρελέ ισχύος (τα πηνία τους), οι ενδεικτικές λυχνίες, οι σειρήνες , βαλβίδες κλπ.
Τις εξόδους τις χαρακτηρίζουμε με το γράμμα Q ή Ο και με ένα αύξοντα αριθμό ανάλογα σε ποια έξοδο του PLC θα το βάλουμε, δηλαδή Q1, Q2, Q3…κοκ.
ΠΡΟΣΟΧΗ: Τα βοηθητικά ρελέ που τα θεωρούμε βοηθητικές μνήμες, δεν είναι υλικά που θα τα τοποθετήσουμε αυτούσια όπως στον κλασσικό αυτοματισμό, αλλά περιέχονται μέσα στο PLC. To ίδιο συμβαίνει με τα χρονικά και τα counter.
Δηλαδή θέλω να πω ότι για να δημιουργήσουμε έναν αυτοματισμό με PLC δεν θα αγοράσουμε βοηθητικά ρελέ, χρονικά και counter. Όλα αυτά περιέχονται μέσα στο PLC.

Έτσι τα βοηθητικά ρελέ είναι θέσεις μνήμης στις οποίες αποθηκεύονται ενδιάμεσες λογικές καταστάσεις και πληροφορίες. Τα χαρακτηρίζουμε σαν Markers ή flags με το γράμμα Μ ή F και με ένα αύξοντα αριθμό, δηλαδή Μ1, Μ2, Μ3 κοκ.
Τα χρονικά τα χαρακτηρίζουμε με το γράμμα Τ και με ένα αύξοντα αριθμό, δηλαδή Τ1, Τ2, Τ3 κοκ.
Τα counters τα χαρακτηρίζουμε με το γράμμα C και με ένα αύξοντα αριθμό, δηλαδή C1, C2, C3 κοκ.

Ας μετατρέψουμε τα πρώτα μας κυκλώματα

ΠΑΡΑΔΕΙΓΜΑ 1

Στο παρακάτω κύκλωμα (σχήμα 1) έχουμε 3 διακόπτες σε σειρά S1, S2, S3 και μια λάμπα, δηλαδή έχουμε 3 εισόδους (3 διακόπτες) και 1 έξοδο (λάμπα).
 
Χαρακτηρίζουμε τις εισόδους σαν Ι1, Ι2, Ι3 και την έξοδο σαν Q1
Η λάμπα θα ανάψει όταν και οι τρεις διακόπτες θα κλείσουν, δηλαδή το Q1 θα πάρει σήμα 1 όταν και οι τρεις διακόπτες δώσουν σήμα 1.
Όταν έχουμε τέτοια στοιχεία συνδεδεμένα σε σειρά τότε τα βάζουμε σαν εισόδους σε μια πύλη AND (3 διακόπτες) και την έξοδο της πύλης την οδηγούμε στην έξοδο του κυκλώματος (λάμπα) όπως φαίνεται στο παρακάτω σχήμα 1. Παρατηρείστε ότι η μετατροπή του κυκλώματος σε γλώσσα FBD είναι η ίδια είτε οι διακόπτες στο αρχικό κύκλωμα είναι κλειστοί είτε είναι ανοικτοί (σχήματα 1α και 1β).

ΠΑΡΑΔΕΙΓΜΑ 2

Στο παρακάτω κύκλωμα  (σχήμα 2) έχουμε 3 διακόπτες παράλληλα  S1, S2, S3 και μια λάμπα, δηλαδή έχουμε 3 εισόδους (3 διακόπτες) και 1 έξοδο (λάμπα).
 
Χαρακτηρίζουμε τις εισόδους σαν Ι1, Ι2, Ι3 και την έξοδο σαν Q1
Η λάμπα θα ανάψει όταν ένας (τουλάχιστον) οποιοσδήποτε από τους τρεις διακόπτες θα κλείσει , δηλαδή το Q1 θα πάρει σήμα 1 όταν ένας (τουλάχιστον) οποιοσδήποτε από τους τρεις διακόπτες δώσει σήμα 1.
Όταν έχουμε τέτοια στοιχεία συνδεδεμένα παράλληλα τότε τα βάζουμε σαν εισόδους σε μια πύλη OR (3 διακόπτες) και την έξοδο της πύλης την οδηγούμε στην έξοδο του κυκλώματος (λάμπα) όπως φαίνεται στο παρακάτω σχήμα 2.

ΠΑΡΑΔΕΙΓΜΑ 3

Στο παρακάτω κύκλωμα (σχήμα 3) έχουμε 2 διακόπτες σε σειρά S1, S2 και αυτοί είναι παράλληλα συνδεδεμένοι με ένα άλλο διακόπτη  S3, καθώς και μια λάμπα, δηλαδή έχουμε 3 εισόδους (3 διακόπτες) και 1 έξοδο (λάμπα).
 
Ένας κανόνας που θα πρέπει να έχουμε υπόψη μας είναι ότι σε κάθε κλάδο του κυκλώματος αρχίζουμε (ΑΝ ΜΠΟΡΟΥΜΕ) από τα στοιχεία που είναι συνδεδεμένα παράλληλα βάζοντάς τα σε μια πύλη OR. Σε αυτό το παράδειγμα δεν μπορούμε.
 
Χαρακτηρίζουμε τις εισόδους σαν Ι1, Ι2, Ι3 και την έξοδο σαν Q1.
Η λάμπα θα ανάψει όταν και οι δύο διακόπτες  S1 και S2 θα κλείσουν ή όταν κλείσει μόνο ο διακόπτης S3.
Σε αυτή την περίπτωση θα πάρουμε μια πύλη AND με εισόδους τους δύο διακόπτες S1, S2 που είναι συνδεδεμένοι σε σειρά.
Στη συνέχεια θα πάρουμε μια πύλη OR με εισόδους την έξοδο της AND και το διακόπτη S3. Η έξοδος της OR θα δώσει στο Q1 όπως φαίνεται στο παρακάτω σχήμα 3.

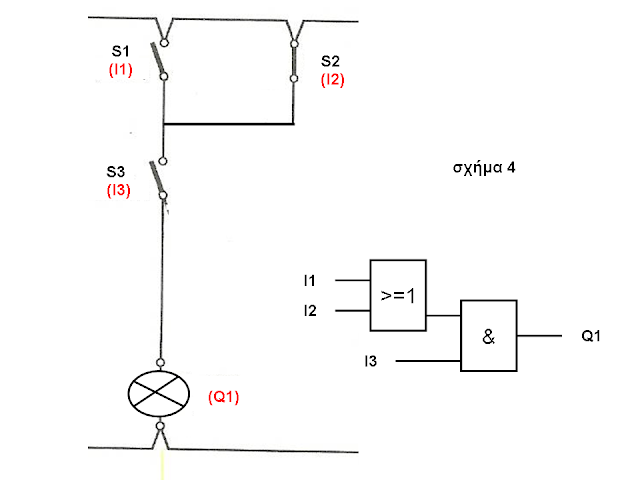
ΠΑΡΑΔΕΙΓΜΑ 4

Στο παρακάτω κύκλωμα (σχήμα 4) έχουμε 2 διακόπτες παράλληλα S1, S2 και αυτοί είναι σε σειρά συνδεδεμένοι με ένα άλλο διακόπτη  S3, καθώς και μια λάμπα, δηλαδή έχουμε 3 εισόδους (3 διακόπτες) και 1 έξοδο (λάμπα).

Θυμίζω τον κανόνα που θα πρέπει να έχουμε υπόψη μας είναι ότι σε κάθε κλάδο του κυκλώματος αρχίζουμε (ΑΝ ΜΠΟΡΟΥΜΕ) από τα στοιχεία που είναι συνδεδεμένα παράλληλα βάζοντάς τα σε μια πύλη OR. Σε αυτό το παράδειγμα μπορούμε.
 
Χαρακτηρίζουμε τις εισόδους σαν Ι1, Ι2, Ι3 και την έξοδο σαν Q1
Η λάμπα θα ανάψει όταν ένας από τους δύο διακόπτες  S1 και S2 θα κλείσει και μαζί με την προηγούμενη συνθήκη όταν κλείσει και ο διακόπτης S3.
Σε αυτή την περίπτωση θα πάρουμε μια πύλη OR  με εισόδους τους δύο διακόπτες S1, S2 που είναι συνδεδεμένοι παράλληλα.
Στη συνέχεια θα πάρουμε μια πύλη AND με εισόδους την έξοδο της OR και το διακόπτη S3. H έξοδος της AND θα δώσει στο Q1 όπως φαίνεται στο παρακάτω σχήμα 4.

ΠΑΡΑΔΕΙΓΜΑ 5

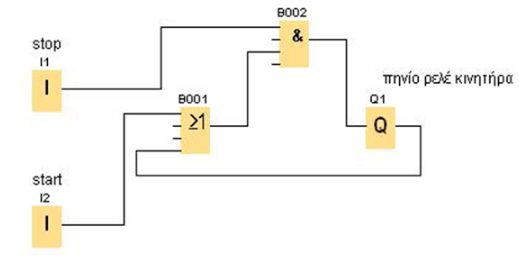
Μετά από αυτά ας προχωρήσουμε στο παρακάτω ολοκληρωμένο κύκλωμα ενός απλού αυτόματου κινητήρα με start-stop. Δεν έχουμε βάλει το θερμικό και θα δούμε μετά και αυτή την περίπτωση. Το κύκλωμα αποτελείται από ένα κλάδο (σχήμα 5)

Έχω δύο εισόδους, τα μπουτόν stop S1 και start S2 και τις οποίες χαρακτηρίζω σαν Ι1 και Ι2 αντίστοιχα και επίσης μια έξοδο, το πηνίο του ρελέ ισχύος Κ1Μ που την χαρακτηρίζω σαν Q1.

Εκτός από αυτά βλέπω ότι έχω και μια βοηθητική επαφή (13-14) του ρελέ ισχύος την οποία θα πρέπει να χαρακτηρίσω και αυτή.
Όλες τις βοηθητικές επαφές που ανήκουν σε ένα ρελέ ισχύος ή χρονικό ή βοηθητικό ρελέ τις χαρακτηρίζω όπως ακριβώς έχω χαρακτηρίσει και τα ίδια τα ρελέ ισχύος, χρονικά, βοηθητικά ρελέ.
Δηλαδή επειδή το ρελέ ισχύος Κ1Μ το έχω χαρακτηρίσει σαν Q1, τότε και τη βοηθητική του επαφή θα τη χαρακτηρίσω σαν Q1.

Οπότε ας προχωρήσουμε στη μετατροπή του κυκλώματος σε γλώσσα FBD.
 
Θυμίζω τον κανόνα που θα πρέπει να έχουμε υπόψη μας είναι ότι σε κάθε κλάδο του κυκλώματος αρχίζουμε (ΑΝ ΜΠΟΡΟΥΜΕ) από τα στοιχεία που είναι συνδεδεμένα παράλληλα βάζοντάς τα σε μια πύλη OR.
Δηλαδή στο κύκλωμά μας ξεκινάμε από τα δύο παράλληλα στοιχεία τα οποία είναι το μπουτόν start και η βοηθητική επαφή 13-14 του ρελέ ισχύος Κ1Μ.
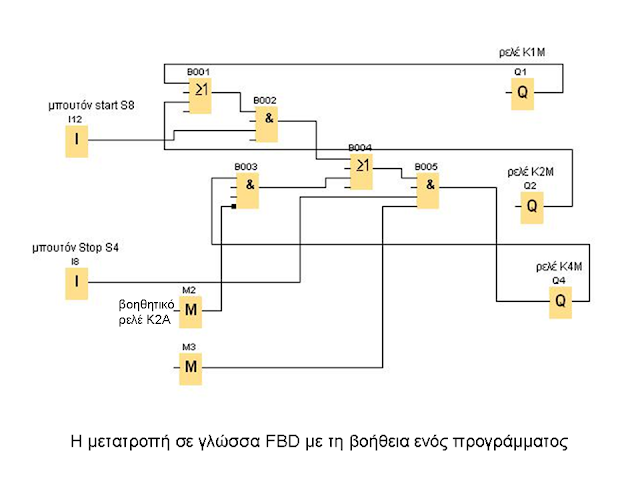
Παίρνω λοιπόν μια πύλη OR με εισόδους Ι2 (start) και Q1 (βοηθητική επαφή 13-14).
Στη συνέχεια παίρνω μια πύλη AND με εισόδους το Ι1 (stop) και την έξοδο της πύλης OR. H έξοδος της AND θα δώσει στο Q1 (πηνίο ρελέ ισχύος Κ1Μ).

H μετατροπή σε γλώσσα FBD με τη βοήθεια ενός προγράμματος φαίνεται στο παρακάτω σχήμα.

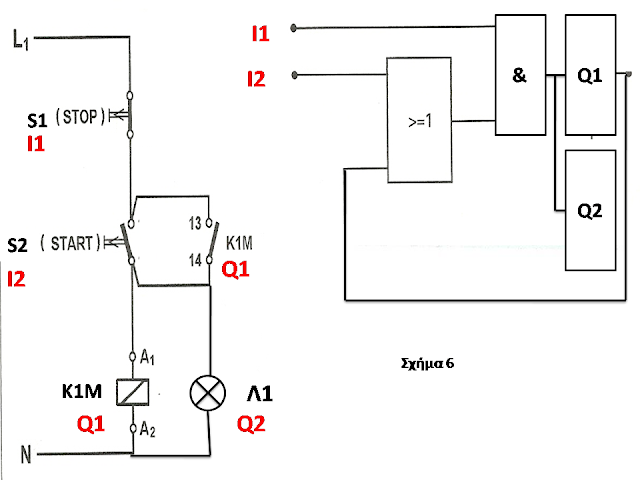
ΠΑΡΑΔΕΙΓΜΑ 6

Στο προηγούμενο κύκλωμα του σχήματος  5 ας προσθέσουμε και μια ενδεικτική λυχνία Λ1 που θα ανάβει όταν δουλεύει ο κινητήρας, δηλαδή όταν οπλίζει το ρελέ ισχύος Κ1Μ, την οποία θα χαρακτηρίσω σαν έξοδο Q2 (σχήμα 6).
 
Σε αυτή την περίπτωση αφού κάνω ακριβώς ότι έκανα στο προηγούμενο κύκλωμα, η έξοδος της τελικής πύλης AND θα δώσει εκτός από το Q1 (πηνίο ρελέ ισχύος Κ1Μ) KAI στο Q2 (ενδεικτική λυχνία Λ1). Δηλαδή το πηνίο Q1 και η ενδεικτική λυχνία Q2 ενεργοποιούνται ταυτόχρονα.

ΠΑΡΑΔΕΙΓΜΑ 7

Στο προηγούμενο κύκλωμα του σχήματος 6 ας προσθέσουμε ακόμα μια ενδεικτική λυχνία Λ2 (την οποία θα χαρακτηρίσω σαν Q3) που θα ανάβει όταν δεν δουλεύει ο κινητήρας και θα σβήνει όταν δουλεύει, μέσω μιας κλειστής βοηθητικής επαφής (21-22) του ρελέ ισχύος Κ1Μ την οποία χαρακτηρίζω και αυτή σαν Q1 μιας και ανήκει στο ρελέ Κ1Μ (σχήμα 7).
 

Σε αυτή την περίπτωση το κύκλωμά μου αποτελείται από δύο κλάδους (σχήμα 7).
Ο πρώτος κλάδος περιέχει το προηγούμενο κύκλωμα που περιλαμβάνει το μπουτόν stop, το μπουτόν start, την ανοικτή βοηθητική επαφή 13-14, το πηνίο του ρελέ ισχύος Κ1Μ και την ενδεικτική λυχνία Λ1.
Ο δεύτερος κλάδος περιλαμβάνει την κλειστή βοηθητική επαφή 21-22 και την ενδεικτική λυχνία Λ2.

Για τον πρώτο κλάδο κάνω ακριβώς τα ίδια με το προηγούμενο παράδειγμα.
Για τον δεύτερο κλάδο δεν χρειάζομαι καμιά πύλη γιατί δεν έχω στοιχεία συνδεδεμένα σε σειρά ή παράλληλα. Έχω μόνο το Q1 (κλειστή βοηθητική επαφή 21-22)  που δίνει απευθείας στο Q3 (ενδεικτική λυχνία Λ2)

ΠΡΟΣΟΧΗ: Σε αυτή την περίπτωση έχω δύο βοηθητικές επαφές, μια ανοικτή (13-14) και μια κλειστή (21-22) που ανήκουν στο ίδιο ρελέ ισχύος Κ1Μ και τις οποίες και τις δύο τις έχω χαρακτηρίσει σαν Q1.
Επειδή όμως το πρόγραμμα σε αυτή την περίπτωση θα πρέπει να ξεχωρίζει ποια βοηθητική επαφή είναι ανοικτή και ποια κλειστή υπάρχει ο παρακάτω κανόνας:
Σε ένα ρελέ που έχει ανοικτές και κλειστές επαφές και το οποίο έχω χαρακτηρίσει σαν Q1, τις ανοικτές επαφές τις χαρακτηρίζω σαν Q1 και τις κλειστές σαν Q1(NOT).
Στο παράδειγμά μας δηλαδή, στο δεύτερο κλάδο η  Q1 (κλειστή βοηθητική επαφή 21-22) θα δώσει στο Q3 (ενδεικτική λυχνία Λ2) αφού προηγουμένως περάσει από μια πύλη NOT όπως φαίνεται στο παρακάτω σχήμα 7.

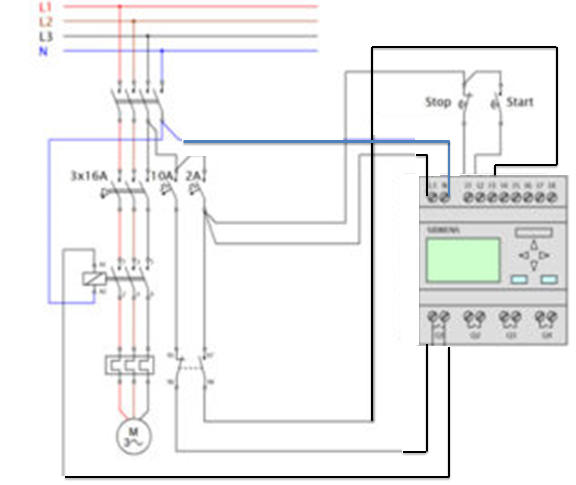
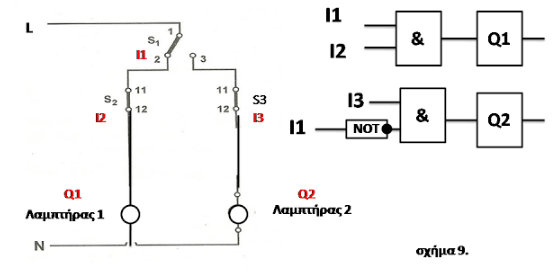
ΠΑΡΑΔΕΙΓΜΑ 8

Στο κύκλωμα του σχήματος 5 (παράδειγμα 5) του απλού αυτόματου διακόπτη ενός κινητήρα ας προσθέσουμε και το θερμικό που λέγαμε το οποίο έχει δύο βοηθητικές επαφές. Μια κλειστή (95-96) που είναι πριν το μπουτόν stop και μια ανοικτή (97-98) που δίνει σε μια ενδεικτική λυχνία Λ1 που ανάβει όταν πέσει το θερμικό (σχήμα 8).

Σε αυτή την περίπτωση θα συνδέσω σαν είσοδο στο PLC την ανοικτή επαφή (97-98), ενώ την κλειστή (95-96) θα τη συνδέσω στη φάση που τροφοδοτεί τις εξόδους του PLC. ‘Ετσι εξασφαλίζουμε και μηχανική διακοπή των εξόδων σε περίπτωση που π.χ κολλήσει το ρελέ εξόδου Q1 του PLC.

 
Σε αυτή την περίπτωση όπως και στην προηγούμενη παρόλο που πρόκειται για είσοδο (επαφές θερμικού ) και όχι για έξοδο (βοηθητικές επαφές ρελέ), επειδή το πρόγραμμα θα πρέπει να καταλάβει τη διαφορά των δύο επαφών του θερμικού, θα πρέπει τη μια να τη θεωρήσω σαν Ι3 και την άλλη σαν Ι3(ΝΟΤ). Συνήθως (όχι αναγκαία) παίρνω σαν Ι3 την κλειστή και σαν Ι3(ΝΟΤ) την ανοικτή.
ΠΡΟΣΟΧΗ: Τα μπουτόν start και stop παρόλο που είναι το ένα ανοικτής και το άλλο κλειστής επαφής, επειδή είναι διαφορετικά εξαρτήματα δεν ακολουθούν τον παραπάνω κανόνα.

Τα προηγούμενα ισχύουν και για οποιοδήποτε διακόπτη διπλής επαφής (σχήμα 9).

ΠΑΡΑΔΕΙΓΜΑ 9

Ας δούμε και τα σύμβολα που χρησιμοποιούμε για τα χρονικά στη γλώσσα FBD (σχήμα 10).

Τα παραπάνω ισχύουν για όλα τα είδη των χρονικών.

ΠΑΡΑΔΕΙΓΜΑ 10

Αν καταλάβατε τα παραπάνω μπορείτε να μετατρέψετε σε γλώσσα FBD το 90% των κλασσικών κυκλωμάτων αυτοματισμού. Ας δούμε ένα παράδειγμα που περιέχει αρκετούς από τους παραπάνω κανόνες (σχήμα 11).
Στην συγκεκριμένη εφαρμογή ζητείται να σχεδιαστεί  να μετατραπεί σε γλώσσα FBD το βοηθητικό κύκλωμα τεσσάρων κινητήρων που ελέγχονται από τους ηλεκτρονόμους Κ1Μ, Κ2Μ, Κ3Μ και Κ4Μ οι οποίοι θα πρέπει να λειτουργούν κάτω από τις εξής συνθήκες :

Ο καθένας θα έχει δικό του START, STOP, θερμικό.
Σε περίπτωση που ενεργοποιηθεί ένα θερμικό να σταματούν και οι τέσσερις κινητήρες..
Ο Κ2Μ ξεκινά και αυτόματα 30 sec μετά την ενεργοποίηση του Κ1Μ.
Για να ξεκινήσει  Κ3Μ θα πρέπει να λειτουργεί και ο Κ1Μ και ο Κ2Μ. Στην περίπτωση που δουλεύουν οι Κ1Μ,Κ2Μ και Κ4Μ και πατήσω να ξεκινήσει ο Κ3Μ τότε ο Κ4Μ θα σταματήσει.
Για να ξεκινήσει ο Κ4Μ  θα πρέπει να λειτουργεί  είτε ο Κ1Μ είτε ο Κ2Μ, και ο Κ3Μ να μην δουλεύει
Στη μετατροπή βέβαια, η παραπάνω εξήγηση της λειτουργίας του κυκλώματος δεν έχει καμία σημασία.

Αυτό που μας ενδιαφέρει είναι να χαρακτηρίσουμε τις εισόδους και τις εξόδους του κυκλώματος. Έχουμε λοιπόν:

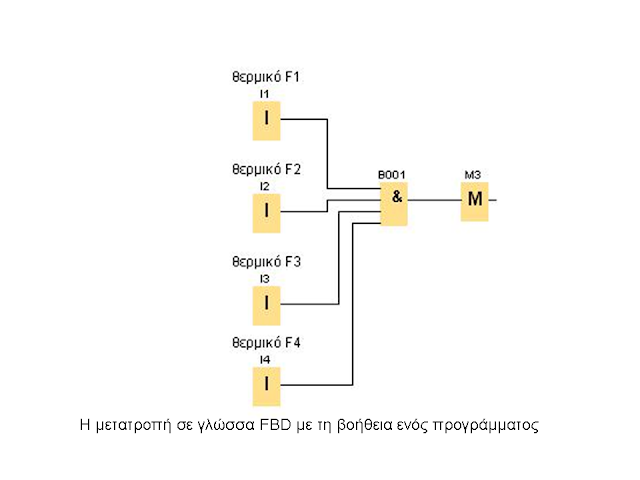
ΕΙΣΟΔΟΙ
Ι1: θερμικό F1
 Ι2: θερμικό F2
 Ι3: θερμικό F3
 Ι4: θερμικό F4
Ι5: stop S1
 Ι6: stop S2
 Ι7: stop S3
 Ι8: stop S4
I9: start S5
 I10: start S6
 I11: start S7
 I12: start S8 

ΕΞΟΔΟΙ
Q1: ρελέ ισχύος Κ1Μ
 Q2: ρελέ ισχύος Κ2Μ
 Q3: ρελέ ισχύος Κ3Μ
 Q4: ρελέ ισχύος Κ4Μ 

Επίσης έχουμε
Μ1: βοηθητικό ρελέ Κ1Α
 Μ2: βοηθητικό ρελέ Κ2Α
Τ1: χρονικό ρελέ Κ1Τ
Τις βοηθητικές επαφές των ρελέ ισχύος, βοηθητικών ρελέ και χρονικού τις χαρακτηρίζω όπως έχω χαρακτηρίσει τα πηνία τους. Όλα αυτά φαίνονται στο σχήμα 12.

Ξεκινάω λοιπόν να μετατρέπω κάθε κλάδο του κυκλώματος σε γλώσσα FBD. Θα παρατηρήσω ότι υπάρχουν 6 κλάδοι και τα θερμικά F1, F2, F3, F4 είναι το κοινό σημείο για κάθε κλάδο. Για το λόγο αυτό θα πρέπει να τα υπολογίζω το ίδιο σε κάθε κλάδο ξεχωριστά. Ένα καλό tip σε αυτές τις περιπτώσεις στις οποίες ένα κομμάτι του κυκλώματος είναι κοινό σε αρκετούς κλάδους είναι αυτό: Μπορούμε αφού αναλύσουμε με πύλες το συγκεκριμένο κομμάτι, το αποτέλεσμα να το οδηγήσουμε σε μια flag M (μια ενδιάμεση μνήμη). Αυτό μας βοηθάει σε μεγάλα προγράμματα να χρησιμοποιούμε το αποτέλεσμα του κοινού κομματιού του κυκλώματος  εύκολα και γρήγορα. Aς δούμε στο παράδειγμά μας.

Τα θερμικά είναι σε σειρά οπότε θα πάρω μια πύλη AND και θα τα βάλω σαν εισόδους. Την έξοδο της AND θα την οδηγήσω λοιπόν σε μια flag M3 {Μ3 γιατί ήδη στο κύκλωμά μου έχω χαρακτηρίσει τα βοηθητικά ρελέ σαν Μ1 και Μ2 (σχήμα 13)}.

Συνεχίζουμε τώρα ξεχωριστά για κάθε κλάδο θυμίζοντας ότι ξεκινάμε (αν μπορούμε) από τα παράλληλα στοιχεία του κυκλώματος.

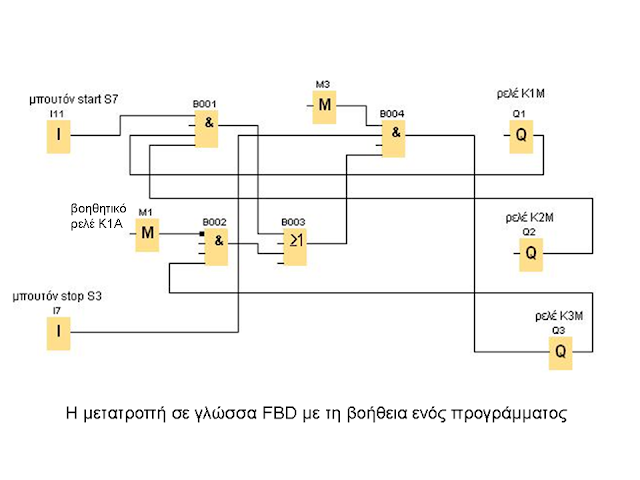
Στον 1o κλάδο (σχήμα 14) έχουμε παράλληλα τα Ι9 (μπουτόν start S5) και Q1 (ΝΟ βοηθητική επαφή του Κ1Μ). Άρα τα βάζουμε σαν εισόδους σε μια πύλη OR.
Στη συνέχεια έχουμε σε σειρά την έξοδο της Μ3 ( όλα τα θερμικά), το Ι5 (μπουτόν stop S1) και την έξοδο της  προηγούμενης OR. Αυτά λοιπόν τα οδηγούμε σαν εισόδους σε μια πύλη AND.
Η έξοδος της AND θα δώσει στο Q1 (πηνίο ρελέ ισχύος Κ1Μ) και στο Τ1 (χρονικό ρελέ Κ1Τ).

Με το ίδιο σκεπτικό μετατρέπουμε και το 2o κλάδο (σχήμα 15).

Στο 3o κλάδο (σχήμα 16) δεν έχουμε αυτούσια (μόνα τους) παράλληλα στοιχεία. Έχουμε τα Ι11, Q1, Q2 σε σειρά τα οποία θα τα οδηγήσουμε σαν εισόδους σε μια πύλη AND.
Έχουμε τα Q3 και Μ1 σε σειρά τα οποία και αυτά θα τα οδηγήσουμε σαν εισόδους σε μια άλλη πύλη AND. Προσοχή όμως εδώ. Η Μ1 είναι NC επαφή και θα πρέπει πριν την οδηγήσω στη πύλη AND να την περάσω πρώτα από μια πύλη NOT.
Τώρα πια έχω παράλληλα τα αποτελέσματα των δύο προηγούμενων πυλών AND. Έτσι λοιπόν τις εξόδους των δύο AND θα τις οδηγήσω σαν εισόδους σε μια πύλη OR.
Τέλος θα βάλω σε μια άλλη τρίτη AND εισόδους τα Μ3, Ι7 και την έξοδο της OR. Tην τελική έξοδο αυτής της AND θα τη στείλω στο Q3.

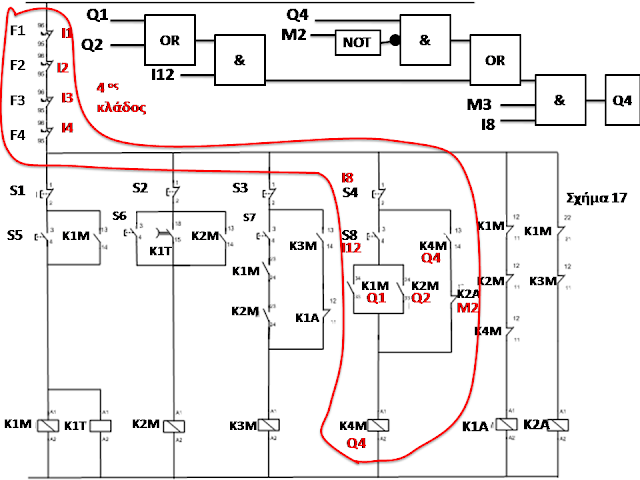
Στο 4o κλάδο (σχήμα 17) ξεκινάμε όπως έχουμε πει από τα παράλληλα στοιχεία  Q1 και Q2 βάζοντάς τα σαν εισόδους σε μια πύλη OR.
Στη συνέχεια σε μια πύλη AND βάζουμε εισόδους  το Ι12 και την έξοδο της προηγούμενης OR.
Σε μια AND βάζουμε εισόδους τα Q4 και M2 προσέχοντας το M2 να το περάσουμε πρώτα από μια πύλη NOT γιατί είναι NC επαφή.
ΣΕ μια OR βάζουμε εισόδους τις εξόδους των δύο προηγούμενων πυλών AND
Τέλος σε μια νέα AND βάζουμε εισόδους τα Μ3, Ι8 και την έξοδο της προηγούμενης OR. Την έξοδο της τελικής AND τη στέλνω στο Q4.

Στο 5o κλάδο (σχήμα 18) τα πράγματα είναι απλά μιας και έχουμε στοιχεία μόνο σε σειρά οπότε σε μια πύλη AND βάζουμε εισόδους τα Μ3, Q1, Q2, Q4 προσέχοντας τα Q1, Q2, Q4 να τα περάσουμε πρώτα από μια πύλη NOT γιατί είναι NC επαφές. Την έξοδο της AND την στέλνουμε στο Μ1.

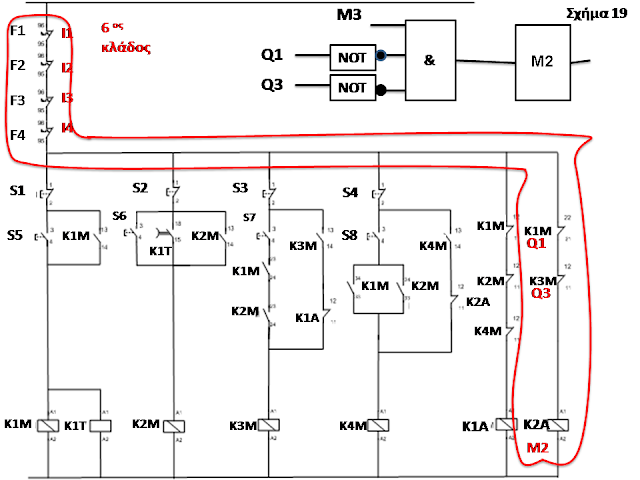
Στο 6o κλάδο (σχήμα 19) τα πράγματα είναι εξίσου απλά μιας και έχουμε στοιχεία μόνο σε σειρά οπότε σε μια πύλη AND βάζουμε εισόδους τα Μ3, Q1, Q3 προσέχοντας τα Q1, Q3 να τα περάσουμε πρώτα από μια πύλη NOT γιατί είναι NC επαφές. Την έξοδο της AND την στέλνουμε στο Μ2.

Η ολοκληρωμένη μετατροπή όλου του κυκλώματος με τη βοήθεια ενός προγράμματος φαίνεται στο επόμενο σχήμα:

Ας δούμε και δυο περιπτώσεις πολύπλοκων κυκλωμάτων

ΠΑΡΑΔΕΙΓΜΑ 11

Στο παράδειγμα του σχήματος 20 το κύκλωμα μπορεί να αναλυθεί σε δύο επιμέρους τμήματα .

Η μετατροπή τώρα των δύο επιμέρους κυκλωμάτων είναι νομίζω εύκολη και μπορεί να την κάνει ο καθένας.

ΠΑΡΑΔΕΙΓΜΑ 12

Μια τέτοια όπως του προηγούμενου παραδείγματος 11 κλασσική περίπτωση πολύπλοκου κυκλώματος είναι ο διακόπτης αστέρα-τριγώνου  που βλέπετε στο σχήμα  21 και το οποίο αποτελείται από 6 κλάδους  (1ος κλάδος καταλήγει στο ρελέ του αστέρα, 2ος κλάδος στο χρονικό, 3ος κλάδος στο γενικό ρελέ, 4ος κλάδος  στο ρελέ του τριγώνου, 5ος κλάδος στο λαμπάκι λειτουργίας και 6ος κλάδος στο λαμπάκι πτώσης θερμικού).

Χαρακτηρίζουμε τις εισόδους-εξόδους όπως ξέρουμε(σχήμα 22).

Στο σχήμα 23 το τμήμα 1 του  κυκλώματος είναι κοινό για τα τμήματα 2 και 3 (δηλαδή το τμήμα 1 είναι κοινό για τους κλάδους 1 έως 5).

Αγνοούμε το τμήμα 3 και προχωράμε στη μετατροπή του κυκλώματος σε γλώσσα FBD.

Αγνοούμε τώρα το τμήμα 2 και συνεχίζουμε στη μετατροπή του κυκλώματος σε γλώσσα FBD.

ΠΑΡΑΔΕΙΓΜΑ 13

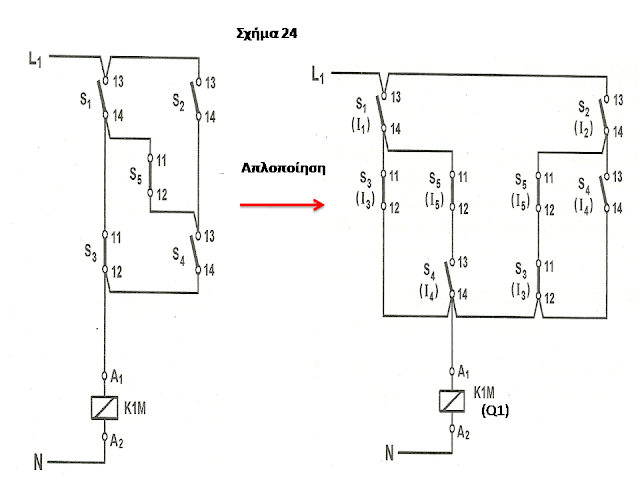
Μια άλλη πολύπλοκη συνδεσμολογία είναι αυτή του σχήματος 24 που λέγεται συνδεσμολογία γέφυρας και στην οποία κάνουμε απλοποίηση του κυκλώματος. Μετά την απλοποίηση είναι και σε αυτό εύκολη η μετατροπή σε γλώσσα FBD.

Στα προηγούμενα ασχοληθήκαμε με τη μετατροπή κυκλωμάτων που περιείχαν ψηφιακές εισόδους και εξόδους, δηλαδή εισόδους και εξόδους που παίρνουν τιμή ‘’0’’ ή ‘’1’’.
Τα PlC όμως μπορούν να καλύψουν πλήρως και τα συστήματα αυτόματου ελέγχου, όπως είναι οι αναλογικοί έλεγχοι θερμοκρασίας, πίεσης, στροφών κινητήρων κ.λ.π. Αυτό γίνεται με τη δυνατότητα των PLC να δέχονται και να επεξεργάζονται αναλογικές εισόδους, όπως και να παρέχουν αναλογικές εξόδους. Το PLC μετατρέπει τις αναλογικές τιμές των εισόδων σε ψηφιακές τιμές και στη συνέχεια επεξεργάζεται τις τιμές αυτές αξιοποιώντας τις δυνατότητες για επεξεργασία ψηφιακών αριθμών όπως είδαμε.

Άρθρο του καθηγητή Τάσου Αντωνάκη-Ηλεκτρολόγου Μηχανικού ΤΕ-Εκπαιδευτικού 1ης ΕΠΑΣ ΟΑΕΔ ΘΕΣΣΑΛΟΝΙΚΗΣ...Δημοσιεύθηκε στην εφημερίδα Εγκαταστάτης